Ngày 1 - Lời giải đề thi HSG quốc gia môn tin học năm 2020

Đề thi ngày 1: PDF.

Link nộp bài: VOI2020. Các bạn cần vào group: VNOI - Vietnam Olympiad in Informatics ở codeforces trước nếu không vào được link contest.

Với các bài, nếu đề quá dài mình sẽ tóm tắt lại đại ý trước khi đi vào lời giải. Mình sẽ chủ yếu đi vào lời giải cho sub cuối cùng, nhưng sẽ nói sơ qua các cách vét điểm.

• Bài 1
  • Lời giải
• Bài 2
  • Tóm tắt đề bài
  • Lời giải
  • Nhận xét
• Bài 3
  • Tóm tắt đề bài
  • Lời giải
  • Nhận xét
• Nhận xét ngày 1

Bài 1: BONUS

• Tag: DP

Lời giải

Subtask 1: \(n \le 300, k \le 2\)

Với \(k\) khá nhỏ, ta hoàn toàn có thể backtrack cách chọn, độ phức tạp: \(O(5^k)\). Cách code có thể đơn giản như sau:

//hàm calc(l, r, k) trả về giá trị tối ưu khi ta xử lý đoạn con [l, r] và còn lại k lượt chọn. Kết quả là calc(1, n, k)
//hàm cost(x, y) trả về giá trị khi chọn cặp 2 lá bài x và y, đơn giản nó là abs(a[x] - a[y])
long long calc(int l, int r, int k) {
    if (l > r) {
        if (k == 0) return 0;
      	//vì đề yêu cầu chọn ĐÚNG k cặp, nên nếu vẫn còn cách chọn thì trạng thái này không thỏa mãn
      	//do đó ta return 1 giá trị cực bé để không bao giờ lấy kết quả này.
        return -INF;
    }
    long long best = -INF;
    if (l + 1 <= r) {
        //thực hiện cách chuyển 1:
        best = calc(l + 2, r, k - 1) + cost(l, l + 1);
        //thực hiện cách chuyển 2:
        best = calc(l, r - 2, k - 1) + cost(r, r - 1);
        //thực hiện cách chuyển 3:
        best = calc(l + 1, r - 1, k - 1) + cost(l, r);
    }
    //thực hiện cách chuyển 4:
    best = max(best, calc(l + 1, r, k));
    //thực hiện cách chuyển 5:
    best = max(best, calc(l, r - 1, k));
    return best;
}

Cách code trên là 1 cách code backtrack, tất nhiên vẫn còn rất nhiều cách backtrack khác nhưng mình dùng cách này để dễ dàng tối ưu hơn.

Subtask 2: \(n \le 30, k = 15\)

Với subtask này mình cũng không biết trâu kiểu gì nữa.

Subtask cuối: \(n \le 300\)

Ở đây ta cải tiến thẳng từ thuật toán ở sub1. Ta nhận thấy hàm calc(l, r, k) sẽ cho ra kết quả như nhau nếu ta truyền vào cùng 1 bộ tham số. Do đó, với mỗi bộ (l, r, k), ta chỉ cần tính 1 lần duy nhất, các lần sau cứ lấy kết quả đã tính, cách này chính là đệ quy có nhớ. Bây giờ với thuật toán trên ta chỉ cần thêm có nhớ vào là AC. Độ phức tạp: \(O(n^2\times k)\), vì ta có số bộ (l, r, k) là \(O(n^2\times k)\), mỗi lần chuyển trạng thái có thể xem là \(O(1)\).

Code tham khảo: BONUS.cpp

Bài 2: BUS

• Tag: DSU, SQRT, DnC

Bài này anh Nghĩa có viết một solution rất đẹp bằng chia để trị, các bạn có thể xem ở: đây. Nhưng mình sẽ viết solution bằng chia căn, xem như là 1 cách tiếp cận khác. Lưu ý rằng dù theo cách tiếp cận nào, bài này là một bài rất khó để cài thuật chuẩn. Bài này có rất nhiều cách làm tham, trong giờ thi, chiến thuật tốt nhất là cài hết thuật tham xong merge các thuật đó lại với nhau, gần như không thể sinh test giết được.

Tóm tắt đề bài:

Cho 2 tập cạnh vô hướng, có trọng số: \(A\) và \(B\). Ta cần chọn ra một tập con các cạnh thuộc \(A\) và tập con các cạnh thuộc \(B\), sao cho:

1. Tổng trọng số của cạnh có trọng số lớn nhất trong mỗi tập con là nhỏ nhất.
2. Sử dụng các cạnh được chọn, ta có thể đi từ đỉnh 1 tới đỉnh \(n\).

Lời giải:

Trong tất cả các subtask: sort các cạnh mỗi loại theo trọng số tăng dần.

Subtask 1: Không có cạnh loại \(B\).

Ta đơn giản thì cần lần lượt thêm cạnh vào cho tới khi có đường đi từ 1 tới \(n\). Dùng disjoin-set có thể dễ dàng làm điều này. Ta cũng có thể dùng chặt nhị phân, dijkstra, …

Subtask 2: \(n, m \le 5000\).

Một nhận xét là khi ta dùng càng nhiều các cạnh loại \(B\), thì ta dùng càng ít các cạnh loại \(A\) (và ngược lại). Tới đây ta có thể dùng 2 con trỏ: Duy trì 1 con trỏ ở các cạnh loại \(A\), duyệt giới hạn các cạnh loại \(B\), sau đó kiểm tra có thể đi được từ 1 tới \(n\) hay không bằng BFS/DFS, rồi dựa vào đó mà cập nhật con trỏ trên các cạnh loại \(A\). Ta thực hiện đúng \(O(n)\) lần BFS/DFS nên độ phức tạp là \(O(n\times (n + m))\)

Subtask 3: Tồn tại cách tối ưu chỉ dùng 1 cạnh loại \(B\).

Do chỉ dùng 1 cạnh loại \(B\), ta nghĩ tới việc duyệt qua các cạnh (u, v) trong tập \(B\), sau đó kiểm tra xem nếu dùng cạnh này thì ta phải dùng cạnh loại \(A\) lớn nhất là bao nhiêu. Để làm được điều đó, ta cần tính ra 2 mảng: \(d1[u] =\) cạnh loại \(A\) lớn nhất cần dùng để đi từ đỉnh 1 tới đỉnh \(u\), \(dn[u]=\) cạnh loại \(A\) lớn nhất cần dùng để đi từ đỉnh \(u\) tới đỉnh \(n\). Việc tính 2 mảng trên có rất nhiều cách, 1 cách đơn giản là dùng Dijkstra.

Sau khi tính được 2 mảng trên, ta đơn giản duyệt qua các cạnh (u, v) thuộc \(B\), cập nhật kết quả với \(max(d1[u], dn[v]) + w(u, v)\), với \(w(u, v)\) là trọng số cạnh (u, v), nên nhớ là cạnh vô hướng nên ta kiểm tra luôn (v, u) nữa.

Subtask 4: \(n, m \le 50000\).

Đây là subtask cuối cùng, việc giải subtask này dựa vào cải tiến thuật toán từ sub2 bằng chia căn (cách này rất khó để code, mình chỉ nêu sơ về ý tưởng):

Ta chia tập các cạnh thuộc \(A, B\) thành các block có độ dài là căn. Sau đó tính mảng \(Fa[i] =\) block nhỏ nhất thuộc \(B\) để khi dùng các block không quá \(i\) thuộc \(A\) và các block không quá \(Fa[i]\) thì có đường đi từ 1 tới \(n\). Việc tính mảng \(Fa\) tương tự như cách làm ở sub2.

Sau khi có mảng \(Fa\), với mỗi block \(i\) ở \(A\), ta cần thực hiện một việc là với mỗi cạnh thuộc block \(i\) ở \(A\), ta cần tính chính xác xem cần dùng các cạnh nào thuộc \(B\), nếu tính trâu thì độ phức tạp quá lớn, nhưng nhờ mảng \(Fa\), ta đã biết số lượng cạnh cần thử không quá lớn (ta chỉ thử các cạnh thuộc block \(Fa[i]\)), chỉ cần thử \(O(\sqrt{m})\) cạnh. Ta lại tiếp tục dùng cách tương tự sub2 để tính tiếp. Với cách này, độ phức tạp để kiểm tra mỗi block là \(O(\sqrt{m} \times n)\), vì ta cần 2 con trỏ \(\sqrt{m}\) cạnh, và thực hiện BFS/DFS để kiểm tra. Ta lại có \(O(\sqrt{m})\) block nữa, do đó thuật này sẽ thành \(O(m\times n)\). Để tối ưu, ta cần tối ưu phần DFS. Ta nhận thấy khi thực hiện mỗi block, ta chỉ quan tâm tới \(O(\sqrt{m})\) đỉnh, vậy nên ta có thể nén các đỉnh này lại, độ phức tạp chỉ còn \(O(\sqrt{m})\) mỗi lần DFS. Chung quy thì độ phức tạp của nó là \(O(\sqrt{m} \times \sqrt{m}) = O(m)\) cho phần này.

Độ phức tạp: \(O(\sqrt{m} \times n)\) để tính mảng \(Fa\), \(O(m)\) cho phần kiểm tra còn lại.

Code tham khảo: BUS.cpp

Nhận xét:

Bài này quá khó để dùng thuật chuẩn, chiến thuật tốt nhất cho bài này trong phòng thi chính là dùng các thuật tham như chặt tam phân. Chứ việc cày offline bài này trong phòng thi không khác gì tự hủy cả. Bài này lúc cài thuật chia căn thì mình cũng sai rất nhiều. May mà có test để debug :v.

Các subtask cho bài này cũng rất khó, vì các subtask không bao nhau, ví dụ như sub 2 và 3 không liên quan gì nhau cả, nên có vét cũng phải cài rất mệt.

Bài 3: STARS

• Tag: DS

Tóm tắt đề bài:

Đa giác chuẩn là đa giác với các đỉnh nằm trong tọa độ grid, không tự cắt và có các cạnh song song với trục tọa độ. Cho \(n\) đa giác chuẩn, mỗi ngày, ta xoay \(n\) đa giác đi 90 độ, hỏi ngày thứ \(d\) thì tổng phần diện tích bị phủ bởi ít nhất 1 đa giác là bao nhiêu.

Lời giải:

Trước khi làm bài này, các bạn nên AC bài AREA trước. Với bài này, ta phải tinh ý nhận ra là với tập điểm cho trước, chỉ dựng được 1 hình đa giác chuẩn duy nhất, nên cái gọi là “diện tích lớn nhất” trong đề là trap. Và việc xoay hình cũng không ảnh hưởng gì tới bài toán.

Subtask 1: Các hình đều là hình vuông, không xoay.

Ừa thì nó là Area đó :v. Nhưng giới hạn nhỏ nên không cần segment tree, chỉ cần sweep line xong đếm trâu.

Subtask 2: Các hình đều là hình vuông, có xoay hình.

Y chang sub1, chỉ là thêm cái xoay hình thôi. Mà như đã nói, bài này cái xoay hình chỉ là phần nhỏ, không ảnh hưởng gì tới thuật toán.

Subtask 3: \(n=2\).

Subtask này mình không nghĩ ra riêng thuật gì để giải cả, và nhiều người mình biết đều bảo thế. Khả năng cao đây là trap.

Subtask 4: \(n \le 1000\)

Tới đây thì ta cứ xoay hình, sau khi xoay xong thì cần dựng đa giác lên, việc dựng đa giác rất đơn giản: Với những tọa độ có cùng tọa độ \(x\), ta sort tăng dần theo tọa độ \(y\), sau đó những điểm ở vị trí lẻ (sau khi sort), sẽ nối với các đỉnh vị trí chẵn (ví dụ: 1-2, 3-4, 5-6, …). Tương tự với các điểm cùng \(y\). Sau đó những cạnh được nối sẽ tạo thành các cạnh của đa giác.

Vấn đề tiếp theo là để làm như bài Area, ta cần biết được cạnh của đa giác là cạnh thêm vào anh cạnh trừ đi, ví dụ với đa giác dưới đây thì cạnh AB là cạnh thêm vào, cạnh CD và EF lại là cạnh xóa đi: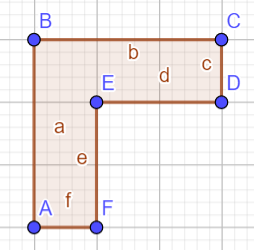

Vậy làm sao ta có thể xác định được đâu là cạnh thêm vào, đâu là cạnh xóa đi? Ta có thể thực hiện duyệt qua từ đỉnh ở trái dưới, sau đó lần lượt men theo các cạnh mà đi hết đa giác, nếu 1 lúc nào đó ta đi hướng lên trên thì cạnh đó là cạnh +1, ngược lại, nếu đi xuống thì là -1. Sau đó thì chỉ cần xử lý trên segment tree như bài AREA là được.

Code tham khảo: STARS.cpp

Nhận xét:

Đây là một bài khó, đã thế đề còn chứa rất nhiều thông tin nhiễu, trap. Nếu để bị đánh lừa, mất thời gian suy nghĩ về những cái trap thì sẽ rất khó khăn.

Nhận xét ngày 1:

Ngoài bài 1 có vẻ rất dễ ra thì bài 2 và 3 đều yêu cầu một khối lượng code rất lớn. Code offline rất dễ nhầm. Bài 2 có thuật toán rất khó nghĩ, bài 3 thì dễ nghĩ ra thuật toán hơn nếu đã biết bài AREA, nhưng lại yêu cầu việc cài khá lằng nhằng, lại nhiều thông tin nhiễu.