Hôm qua mình làm Freecontest gặp một bài dùng chặt nhị phân trên Parabol và mình chặt sai :v Sau khi được thông não thì mình viết bài này một phần để note lại vì sợ quên :))
Vấn đề
- Cho một hàm số F(x) có tập xác định trên đoạn nguyên [a;b], đồ thị có dạng Parabol , tìm cực trị (cực đại hoặc cực tiểu tùy hình dạng hàm) của hàm F(x).
Giải quyết
- Có thể dùng chặt tam phân. Nhưng do F(x) xác định trên đoạn nguyên nên ta có thể dùng chặt nhị phân cho đơn giản :3
- Gọi x0 là cực tiểu (xem như F(x) có cực tiểu cho dễ nói :3) của F(x).
- Để ý là x0 là cực tiểu thì ta có tính chất sau: F(a)>F(a+1)>…>F(x0-1)>F(x0)<F(x0+1)<…<F(b). Từ đó ta có thể nhận thấy x0 chính là vị trí cuối cùng mà F(x0-1)>F(x0) hay vị trí đầu tiên mà F(x0)<F(x0+1), do đó ta có thể chặt nhị phân một cách đơn giản.
Mở rộng vấn đề
- Nhận xét trên chỉ đúng khi hàm F(x) đơn điệu trên [a,x0] và [x0,b] (nghĩa là tăng/giảm nghiêm ngặt), bây giờ nếu hàm F(x) tồn tại một vài đoạn [l,r] sao cho F(l)=F(l+1)=…=F(r) thì việc chặt nhị phân (hay tam phân) đều sẽ không đưa ra kết quả chính xác trong mọi trường hợp (?).
- Ví dụ cụ thể: Cho 2 hàm số L(x) và R(x) đều có tập xác định trên đoạn nguyên [a,b]. Hàm L(x) là hàm không giảm (tăng không nghiêm ngặt), R(x) là hàm không tăng (giảm không nghiêm ngặt). Gọi F(x)= max(L(x),R(x)), tìm cực tiểu của F(x).
- Trong hình dưới đây, màu cam là hàm R(x), màu đen là hàm L(x)
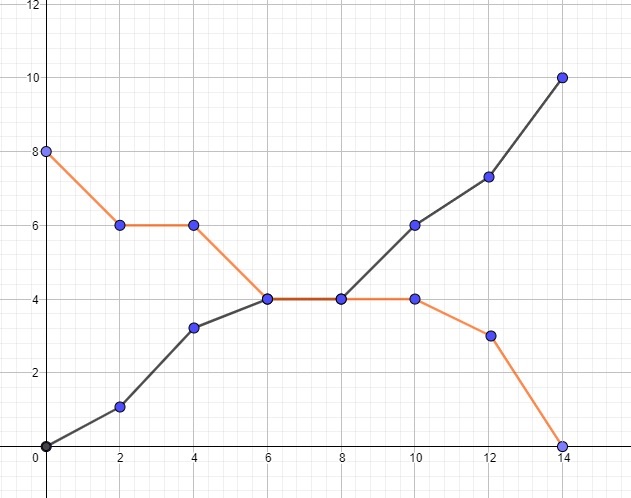 .
. - Hàm F(x) có thể xem như là phần trên của cả 2 đồ thị kia.
- Trong hình dưới đây, màu cam là hàm R(x), màu đen là hàm L(x)
- Cách giải quyết trường hợp này là mình đặt hàm D(x)=R(x)-L(x), D(x) có cùng tập xác định với L(x) và R(x). Dễ dàng chứng minh được D(x) là một hàm không tăng (tổng của 2 hàm không tăng là hàm không tăng). Để F(x) nhỏ nhất ta có thể chặt nhị phân tìm x0 lớn nhất thỏa mãn D(x0)>=0, lúc đó F(x0) là cực tiểu.